Play is often talked about as if it were a relief from serious learning. But for children play is serious learning. Play is really the work of childhood”
—Fred Rogers
When was the last time you played? What did you do…and how did you feel? As adults, we often associate play as the opposite of work, leading us to feel guilty and unproductive for having those few moments of playfulness and joy. Work is supposed to be serious and structured, right? We find this notion to oppose play to work odd because we see play and playfulness exist in almost every activity we do. Play exists in those moments of joy, curiosities, frustrations, breakthroughs, and challenges that we face in our world every single day.
Over the past several years, we have been fortunate enough to observe and learn from several Los Angeles teachers and students. Throughout these experiences, we witnessed and appreciated how learning is almost never a linear experience; it is messy and can be a curiously challenging process before we understand something in the world. This is one of the many reasons why we believe play should never be pitted against work. Play can help students make sense of the messiness that comes with learning new things. It can provide students with a space to engage in creative and inventive ways, including opportunities to explore, apply, share, and reflect on misconceptions and problem solving strategies.
A few months ago, while we were in Nancy’s 5th grade classroom, we saw an example of how playfulness can unfold in a productive, inventive, and joyful way. On this particular day, students were working on a variety of activities and projects around decimal numbers and place value (see sample student work below)
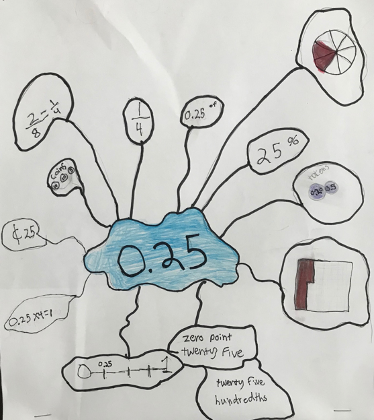
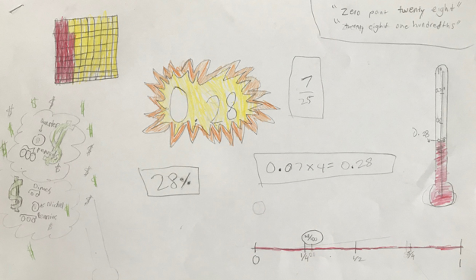
While Nancy was working with her students, she noticed Lauren was struggling to work with a decimal number in her math journal. Nancy uses these math journals for a variety of sense-making activities (i.e to solve problems in or to jot down curiosities or questions). Lauren was brainstorming in her journal how she can represent a decimal number with money. For example, if she was working with the decimal 0.50 she could draw 2 quarters or 5 dimes (or any other combination of coins to make 50 cents). However, Lauren chose to work with the decimal 0.456 and was struggling to figure out which combination of coins she could use to represent this number.
Instead of correcting and pointing out that 0.456 couldn’t be represented in coins, Nancy and Lauren shared the problem with the rest of the class. The students gathered in the front of the room as Nancy wrote the decimal 0.456 on the board. She shared the story of how Lauren was trying to figure out which coins could help represent this number, and opened up the problem to the rest of the class for strategies or ideas.
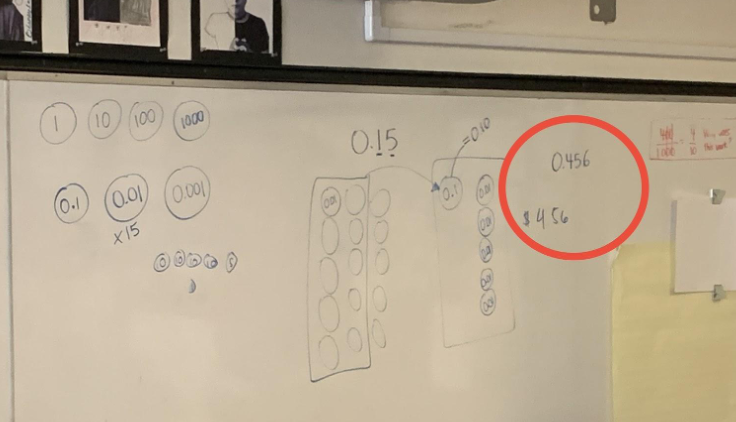
At first, students offered to start with 4 dimes, while others suggested starting with a quarter. There was a mixture of voices as students shouted out suggestions for Lauren. But it didn’t take long before a student named Stanley suddenly realized 0.456 couldn’t be represented with a standard coin. Stanley raised his hand, shared this realization to the class, and then gleefully suggested to Lauren to split a quarter into several parts in order to get 0.006. What was most interesting about this moment was how easy it was for Stanley to come up with the idea to playfully cut a coin into pieces, instead of dismissing Lauren’s problem as impossible and suggesting to come up with a new number that can be represented with money.
Stanley’s suggestion then inspired the rest of the class to come up with different ways to cut up and divide coins in order to make 0.456. Several students giggled and shouted out more ideas to cut up and divide pennies, dimes, and quarters in order to help Lauren find a way to make 0.456. After a few more suggestions from students to divide coins, a student named Ben wondered aloud if perhaps the problem with trying to represent 0.456 was because Lauren was using American currency. Maybe we can use pesos or money from other countries that can make up a number in the thousandths place? Ben’s suggestion then led several students to share different countries and currencies, and how foreign coins could possibly help Lauren come up with 0.456 more easily than dividing American coins into parts.
What struck us the most about this interaction was how playful and fun it was for students to invent ideas and strategies for making money to the thousandths place. Many adults would view this interaction as silly and unproductive, or even worse, an example of students fooling around and not working on math. However, we invite you to think about the mathematical reasoning behind each and every one of the students’ suggestions. In the example of Lauren’s 0.456 decimal, students displayed knowledge of problem solving, division, place value, money, cultural knowledge, and even fractions (breaking coins into parts) in their own meaningful ways. Learning is a process, and making room for these messy and playful interactions as a valid and valuable part of school interactions can cultivate a love for mathematical thinking that leads students to be active in learning and doing math. Math is beautiful, artistic, and varied, and should not be a rigid set of rules for students to follow. Math is a subject that should be fun and playful because when you play with math you create conceptual understanding that is yours to keep.