A mixed-age classroom of kids is working on the second story problem of the year. This multiplication problem is about our principal, Ms. Silva, and her many pizzas:
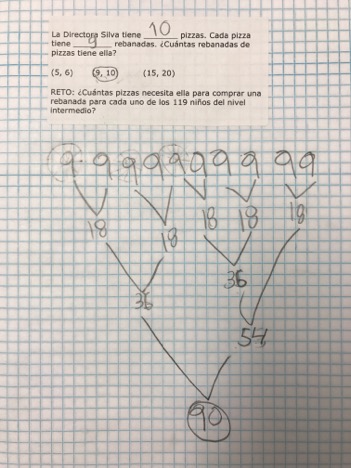
Principal Silva has 9 pizzas. Each pizza has 10 slices. How many slices does she have?
CHALLENGE: How many pizzas does she need to buy to have one slice for each of our 119 Intermediate students?
Today, there is a juicy scenario happening between two of the youngest children that I’ll call Nate and Kate. Nate solved the problem quickly and recorded his thinking with ease.
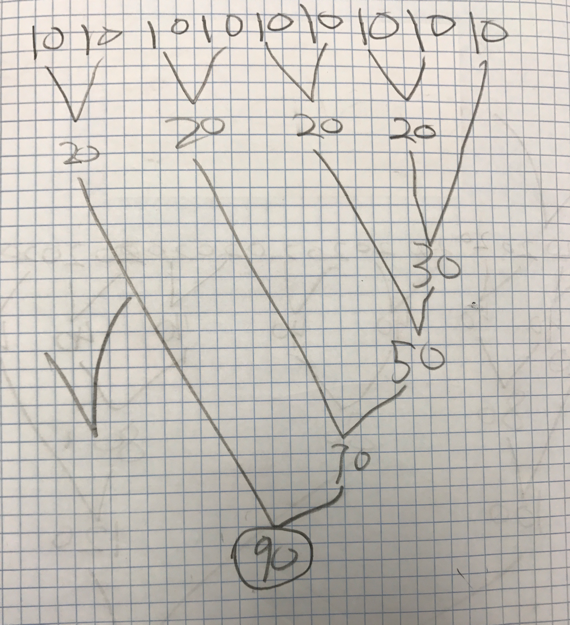
Meanwhile, Kate is working harder to pull out unifix cubes and line them up to represent slices of different pizzas. She asks me twice: “¿Son 9? /Are these all 9?” as she waves her hand over her 10 groups. I respond with another question: “¿Cómo lo podrías comprobar?/ How could you check?” With renewed determination, she recounts each column of 9. She doesn’t simply count one tower of cubes and then compare all the heights – this too, is good information for me. Then Kate begins to count ALL of her towers starting at 1 – she doesn’t start at the bottom of the second tower saying “10, 11, 12…” She’s showing lots of perseverance, and when she counts all of the unifix cubes (90), she then begins to record on her page. Kate’s recording does not actually match what she did and she’s experiencing productive struggles as she adds all of the 9s – using fingers, a 200s chart and even the help of a friend who jumps in while she’s adding 63 + 9 (the words sixty and seventy are confusing for many children in Spanish). After several minutes, she’s got a recording that actually shows a third way of adding nine together ten times. She’s pretty darn sure, now. Yup, Ms. Silva has 90 slices of pizza! Since Kate and Nate happen to be working close to each other I ask them to take a look at each other’s strategies and share what they observe. Their immediate reaction is “Sí, ¡son 90 rebanadas! /Yes, there are 90 slices!”. So I ask them again if there is anything else they notice or wonder. Nate takes the bait. He explains that Kate’s strategy works and his makes sense too but they made different groups. Kate asks, “¿Por qué hiciste grupos de 10?/ Why did you make groups of 10?”. Nate rereads her the problem to show her that each pizza should have 10 slices. However, he and another boy tell her, “No imorta./It doesn’t matter” if she switched the numbers. 9 groups of 10 is the same as 10 groups of 9.
Kate looks dubious… How could it be the same? I ask Nate if he can prove it. Could he use tools or draw a picture to show they are the same? As if by magic, this array comes to him. He draws it on a mini whiteboard. Then, Nate proceeds to rotate it slowly so that Kate can first see 9 rows of 10 (his way) and then 10 rows of 9 (her way), which he counts out for her.
Their other friend writes the following equation on the whiteboard as Nate rotates his orange array for the whole class now. I label the equations the “commutative property” and say we wil continue to talk more about “multiplying numbers in any order” this year.
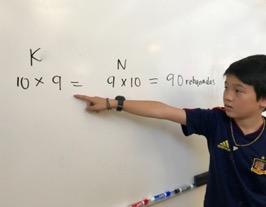
Mysteriously… our warm-up two days later features the commutative property. After a different child suggest rotating the array at the bottom, another student yells excitedly, “¡Eso es lo que hicieron Kate y Nate!” Yes, that’s exactly what Kate and Nate did! Again, I label it the commutative property in Spanish and tell them we will continue to talk about the property this year.
The kids had remembered the property because classmates had shown ownership and agency as mathematicians to begin to understand and name it.
What ideas do you have about fostering ownership and agency in your classroom? What stories will your students tell about grappling with big concepts and new vocabulary?